
El Álgebra de Boole es una estructura algebraica que puede ser considerada desde distintos puntos de vista matemáticos:
Como retículo
El álgebra de Boole es un retículo (A,  , +), donde el conjunto A esta formado por dos elementos A={0, 1}, como retículo presenta las siguientes propiedades, las leyes principales son estas:
, +), donde el conjunto A esta formado por dos elementos A={0, 1}, como retículo presenta las siguientes propiedades, las leyes principales son estas:
1. Ley de Idempotencia:

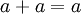
2. Ley de Asociatividad:
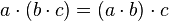
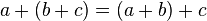
3. Ley de Conmutatividad:
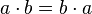
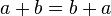
4. Ley de Cancelativo


Como anillo
El Álgebra de Boole tiene Estructura algebraica de Anillo:
Grupo abeliano respecto a (+)
El conjunto A={0,1} es un Grupo abeliano respecto a (+):
1. (+) es una operación interna en A:

2. Es asociativa:
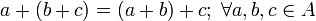
3. Tiene elemento neutro
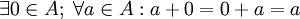
4. Tiene elemento simétrico:

5. es conmutativa:

Grupo abeliano respecto a (·)
El conjunto A={0,1} es un Grupo abeliano respecto a ( ):
):
6. ( ) es una operación interna en A:
) es una operación interna en A:
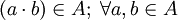
7. Es asociativa:
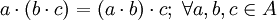
8. Tiene elemento neutro

9. Tiene elemento simétrico:

10. es conmutativa:
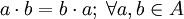
Distributivo
El conjunto A={0,1} es un Grupo abeliano respecto a (+) y ( ) y es distributiva:
) y es distributiva:
11. La operación (+) es distributiva respecto a ( ):
):

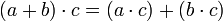
12. La operación ( ) es distributiva respecto a (+):
) es distributiva respecto a (+):
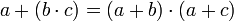
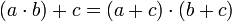
Como resultado podemos decir que el Álgebra de Boole tiene Estructura algebraica de anillo conmutativo y con elemento neutro respecto a las dos operaciones (+) y ( ).
).
Operaciones
Hemos definido el conjunto A = {0,1} como el conjunto universal sobre el que se aplica el álgebra de Boole, sobre estos elementos se definen varias operaciones, veamos las más fundamentales:
Operación suma
| a |
b |
a + b |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
La operación suma (+) asigna a cada par de valores a, b de A un valor c de A:

Su equivalencia en lógica de interruptores es un circuito de dos interruptores en paralelo.

Si uno de los valores de a o b es 1, el resultado será 1, es necesario que los dos sumandos sean 0, para que el resultado sea 0.
Operación producto
| a |
b |
a  b b |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
La operación producto ( ) asigna a cada par de valores a, b de A un valor c de A:
) asigna a cada par de valores a, b de A un valor c de A:
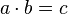
Esta operación en lógica de interruptores es un circuito en serie de dos interruptores
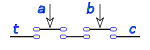
solo si los dos valores a y b son 1, el resultado será 1, si uno solo de ellos es 0 el resultado será 0.
Operación negación
| a |
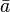 |
| 0 |
1 |
| 1 |
0 |
La operación negación presenta el opuesto del valor de a:

Un interruptor inverso equivale a esta operación:

Operaciones combinadas
| a |
b |
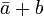 |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
Partiendo de estas tres operaciones elementales se pueden realizar otras más complejas, que podemos representar como ecuaciones booleanas, por ejemplo:

Que representado en lógica de interruptores es un circuito de dos interruptores en paralelo, siendo el primero de ellos inverso.

La distinta secuencia de valores de a y b da los resultados vistos en la tabla de verdad.
Leyes fundamentales
El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano resulta en otra variable del sistema, y este resultado es único.
1. Ley de idempotencia:

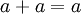
2. Ley de involución:
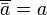
3. Ley conmutativa:
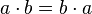
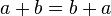
4. Ley asociativa:
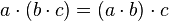
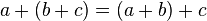
5. Ley distributiva:

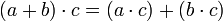
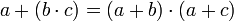
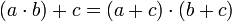

6. Ley de cancelación:


7. Leyes de De Morgan:
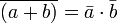
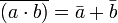
Principio de dualidad
El concepto de dualidad permite formalizar este hecho: a toda relación o ley lógica le corresponderá su dual, formada mediante el intercambio de los operadores unión (suma lógica) con los de intersección (producto lógico), y de los 1 con los 0.
Además hay que cambiar cada variable por su negada. Esto causa confusión al aplicarlo en los teoremas básicos, pero es totalmente necesario para la correcta aplicación del principio de dualidad. Véase que esto no modifica la tabla adjunta.
-
| |
Adición |
Producto |
| 1 |
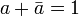 |
 |
| 2 |
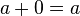 |
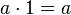 |
| 3 |
 |
 |
| 4 |
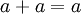 |
 |
| 5 |
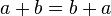 |
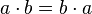 |
| 6 |
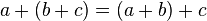 |
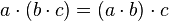 |
| 7 |
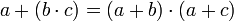 |
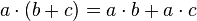 |
| 8 |
 |
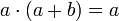 |
| 9 |
 |
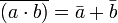 |
Otras formas de notación del álgebra de Boole
En matemática se emplea la notación emplEada hasta ahora ({0,1}, + ,  ) siendo la forma más usual y la más cómoda de representar.
) siendo la forma más usual y la más cómoda de representar.
Por ejemplo las leyes de De Morgan se representan así:

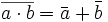
Cuando el álgebra de Boole se emplea en electrónica, suele emplearse la misma denominación que para las puerta lógica AND (Y), OR (O) y NOT (NO), ampliándose en ocasiones con X-OR (O exclusiva) y su negadas NAND (NO Y), NOR (NO O) y X-NOR (equivalencia). las variables pueden representarse con letras mayúsculas o minúsculas, y pueden tomar los valores {0, 1}
Empleando esta notación las leyes de De Morgan se representan:
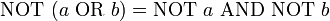

En su aplicación a la lógica se emplea la notación 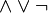 y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
y las variables pueden tomar los valores {F, V}, falso o verdadero, equivalentes a {0, 1}
Con la notación lógica las leyes de De Morgan serian así:
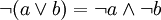

En el formato de Teoría de conjuntos el Álgebra de Boole toma el aspecto: 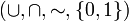
En esta notación las leyes de De Morgan serian así:
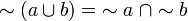
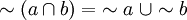
Desde el punto de vista practico existe una forma simplificada de representar expresiones booleanas. Se emplean apóstrofes (') para indicar la negación, la operación suma (+) se representa de la forma normal en álgebra, y para el producto no se emplea ningún signo, las variables se representan, normalmente con una letra mayúscula, la sucesión de dos variables indica el producto entre ellas, no una variable nombrada con dos letras.
La representación de las leyes de De Morgan con este sistema quedaría así, con letra minúsculas para las variables:
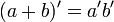

y así, empleando letras mayúsculas para representar las variables:

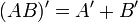
Todas estas formas de representación son correctas, se utilizan de hecho, y pueden verse al consultar bibliografía. La utilización de una u otra notación no modifica el álgebra de Boole, solo su aspecto, y depende de la rama de las matemáticas o la tecnología en la que se este utilizando para emplear una u otra notación.
Álgebra de Boole aplicada a la informática
Se dice que una variable tiene valor booleano cuando, en general, la variable contiene un 0 lógico o un 1 lógico. Esto, en la mayoría de los lenguajes de programación, se traduce en false (falso) o true (verdadero), respectivamente.
Una variable puede no ser de tipo booleano, y guardar valores que, en principio, no son booleanos; ya que, globalmente, los compiladores trabajan con esos otros valores, numéricos normalmente aunque también algunos permiten cambios desde, incluso, caracteres, finalizando en valor booleano. ..
El 0 lógico
El valor booleano de negación suele ser representado como false, aunque también permite y equivale al valor natural, entero y decimal (exacto) 0, así como la cadena "false", e incluso la cadena "0".
El 1 lógico
En cambio, el resto de valores apuntan al valor booleano de afirmación, representado normalmente como true, ya que, por definición, el valor 1 se tiene cuando no es 0. Cualquier número distinto de cero se comporta como un 1 lógico, y lo mismo sucede con casi cualquier cadena (menos la "false", en caso de ser ésta la correspondiente al 0 lógico).
HECHO POR: GONZALEZ HERRERA ELIAS VICENTE